La campana de Gauss, también conocida como la distribución normal, es uno de los conceptos más fundamentales y poderosos en estadística y ciencias. Imagina que tienes un grupo de datos, como las alturas de un grupo de personas. Al graficar esos datos, es probable que obtengas una forma de campana: baja en los extremos y alta en el centro. Esta forma no solo es visualmente atractiva, sino que también tiene profundas implicaciones en cómo entendemos el mundo que nos rodea. La campana de Gauss no solo ayuda a resumir y analizar datos, sino que también proporciona una base para realizar inferencias y predicciones en diversas disciplinas, desde la psicología hasta la ingeniería. En este artículo, exploraremos la importancia de la campana de Gauss, su historia, sus aplicaciones prácticas y cómo influye en la toma de decisiones en la vida cotidiana.
¿Qué es la Campana de Gauss?
La campana de Gauss es una representación gráfica de la distribución normal, que es un tipo de distribución de probabilidad continua. Esta forma de campana es simétrica y se caracteriza por su media, mediana y moda que son iguales. Pero, ¿qué significa esto en términos más simples?
1 Definición y características
La distribución normal es una de las distribuciones más comunes en estadística. Se define por dos parámetros: la media (μ) y la desviación estándar (σ). La media determina la posición del centro de la campana, mientras que la desviación estándar controla la amplitud de la campana. En términos prácticos:
– Media (μ): Es el promedio de todos los datos. En el caso de las alturas, sería la altura promedio del grupo.
– Desviación estándar (σ): Indica cuán dispersos están los datos respecto a la media. Una desviación estándar baja significa que los datos están muy cerca de la media, mientras que una alta indica una mayor dispersión.
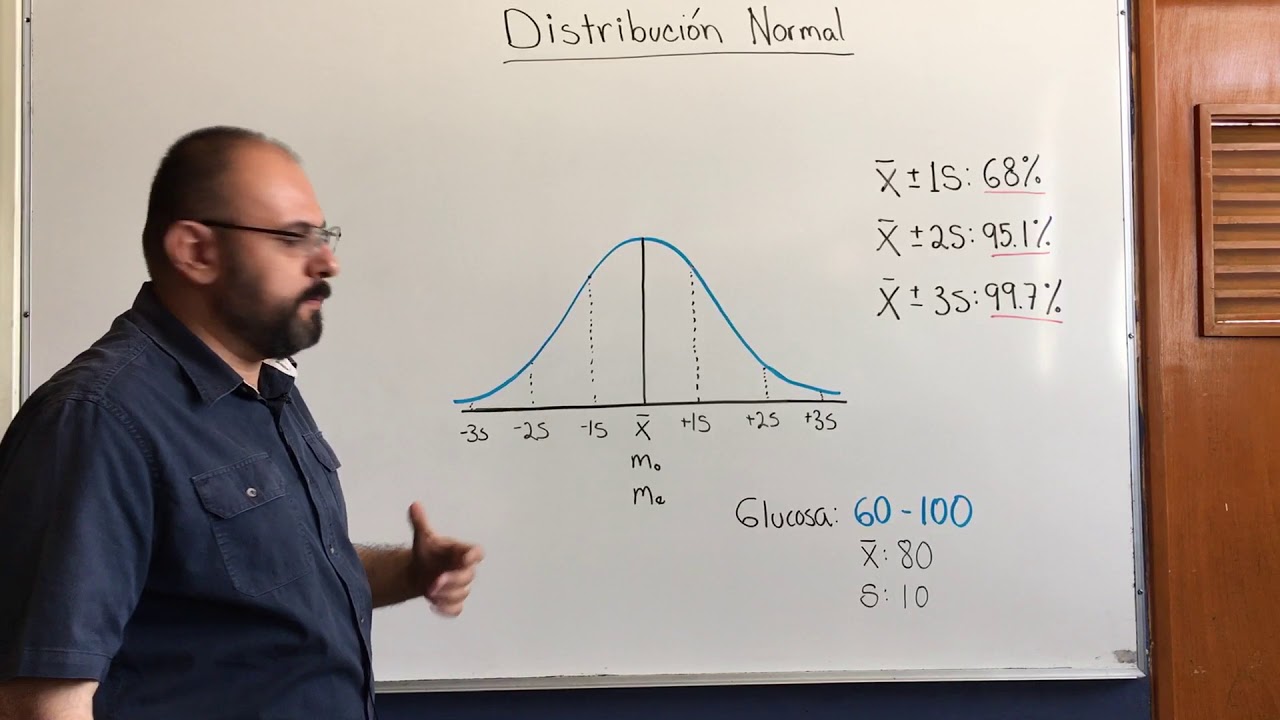
Un aspecto fascinante de la campana de Gauss es que, aproximadamente, el 68% de los datos caerán dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones y el 99.7% dentro de tres. Este principio se conoce como la regla empírica o la regla del 68-95-99.7.
2 Historia y desarrollo
La campana de Gauss recibe su nombre de Carl Friedrich Gauss, un matemático alemán que hizo contribuciones significativas al campo de la estadística en el siglo XIX. Aunque él no fue el primero en describir esta distribución, su trabajo en la teoría de errores y la astronomía ayudó a popularizarla. Su método para ajustar datos experimentales y su enfoque en la media y la desviación estándar sentaron las bases para el análisis estadístico moderno.
A lo largo del tiempo, la campana de Gauss ha evolucionado y se ha integrado en diversas áreas del conocimiento, desde la biología hasta la economía. Su relevancia ha crecido, especialmente en el contexto de la investigación científica y la toma de decisiones basadas en datos.
Aplicaciones de la Campana de Gauss en Estadística
La campana de Gauss es fundamental en estadística por varias razones. Su capacidad para modelar fenómenos naturales y sociales la convierte en una herramienta esencial para investigadores y analistas.
1 Inferencia estadística
La inferencia estadística es el proceso mediante el cual se extraen conclusiones sobre una población a partir de una muestra. La campana de Gauss juega un papel crucial en este proceso. Por ejemplo, si realizamos un estudio sobre las preferencias de un grupo de personas, podemos utilizar la distribución normal para estimar la media de la población y construir intervalos de confianza.
Los intervalos de confianza nos permiten establecer un rango en el que creemos que se encuentra la media de la población. Esto es especialmente útil en la investigación de mercado, donde las empresas necesitan entender las preferencias de sus clientes para tomar decisiones informadas.
2 Pruebas de hipótesis
Las pruebas de hipótesis son otra aplicación importante de la campana de Gauss. En este contexto, se plantea una hipótesis nula y una alternativa, y se utiliza la distribución normal para determinar si hay suficiente evidencia para rechazar la hipótesis nula. Por ejemplo, si una empresa quiere probar si un nuevo producto es mejor que uno anterior, puede usar pruebas de hipótesis para analizar los datos de ventas y determinar si las diferencias son estadísticamente significativas.
La campana de Gauss proporciona un marco para calcular valores p, que indican la probabilidad de observar los resultados obtenidos si la hipótesis nula fuera cierta. Esto ayuda a los investigadores a tomar decisiones basadas en evidencia y a evitar conclusiones erróneas.
3 Control de calidad
En el ámbito industrial, la campana de Gauss se utiliza para el control de calidad. Los procesos de producción suelen seguir una distribución normal, y al monitorizar la variabilidad de los productos, las empresas pueden asegurarse de que cumplen con los estándares establecidos. Por ejemplo, en la fabricación de automóviles, la altura de los componentes debe estar dentro de ciertos límites para garantizar que encajen correctamente. Utilizando la distribución normal, los ingenieros pueden identificar y corregir problemas en el proceso de producción.
La Campana de Gauss en las Ciencias Sociales
Las ciencias sociales, como la psicología y la sociología, también se benefician enormemente de la campana de Gauss. La naturaleza humana y los comportamientos sociales tienden a seguir patrones que pueden ser modelados utilizando esta distribución.
1 Estudios psicológicos
En psicología, muchas pruebas de inteligencia y habilidades cognitivas están diseñadas para seguir una distribución normal. Esto significa que la mayoría de las personas obtendrán puntajes cercanos a la media, mientras que solo unas pocas tendrán puntajes extremadamente altos o bajos. Esta propiedad permite a los psicólogos comparar el rendimiento de un individuo con el de la población general.
Por ejemplo, al aplicar un test de IQ, se espera que la mayoría de los resultados se concentren alrededor de un puntaje de 100, con menos personas obteniendo puntajes muy altos o muy bajos. Esto ayuda a los investigadores a entender la variabilidad en las capacidades cognitivas y a identificar posibles excepciones.
2 Análisis de encuestas
Las encuestas son una herramienta común en las ciencias sociales para recoger datos sobre actitudes, opiniones y comportamientos. Al analizar los resultados, es frecuente que los datos se distribuyan de manera normal. Esto permite a los investigadores hacer inferencias sobre la población a partir de la muestra, utilizando la campana de Gauss para resumir y presentar los hallazgos de manera clara.
Por ejemplo, si se realiza una encuesta sobre la satisfacción laboral, es probable que la mayoría de los encuestados se sitúen en el medio de la escala de satisfacción, mientras que unos pocos se sientan extremadamente satisfechos o insatisfechos. Este patrón ayuda a las empresas a entender mejor la moral de sus empleados y a realizar mejoras donde sea necesario.
Limitaciones de la Campana de Gauss
A pesar de su utilidad, la campana de Gauss no es perfecta y presenta algunas limitaciones que es importante considerar.
1 No todos los datos son normales
Una de las principales limitaciones de la campana de Gauss es que no todos los conjuntos de datos siguen una distribución normal. Existen distribuciones sesgadas o con colas pesadas que no se ajustan bien a la campana de Gauss. Por ejemplo, los ingresos en una población a menudo siguen una distribución log-normal, donde unos pocos individuos tienen ingresos extremadamente altos.
Cuando se asume incorrectamente que los datos son normales, se pueden cometer errores en el análisis y en la interpretación de los resultados. Por lo tanto, es crucial realizar pruebas de normalidad antes de aplicar métodos estadísticos que dependan de esta suposición.
2 Sensibilidad a los valores atípicos
La campana de Gauss es sensible a los valores atípicos, que son observaciones que se desvían significativamente del resto de los datos. Un solo valor atípico puede distorsionar la media y la desviación estándar, afectando la interpretación de los resultados. Por ejemplo, si se mide el ingreso de un grupo de personas y uno de ellos es un multimillonario, la media se verá inflada, lo que no reflejará la realidad de la mayoría de los encuestados.
Para abordar este problema, se pueden utilizar medidas robustas como la mediana y el rango intercuartílico, que son menos afectadas por valores atípicos. Esto permite obtener una representación más precisa de los datos.
La Campana de Gauss en la Vida Cotidiana
La campana de Gauss no solo se limita a la estadística y las ciencias; su influencia se extiende a muchos aspectos de nuestra vida cotidiana.
1 Toma de decisiones
La campana de Gauss nos ayuda a tomar decisiones informadas al analizar datos. Por ejemplo, al considerar la compra de un coche, podemos ver las calificaciones de seguridad y rendimiento. Si la mayoría de los coches tienen calificaciones cercanas a la media, es probable que elijamos uno que esté dentro de ese rango, evitando aquellos con calificaciones extremas.
La comprensión de cómo se distribuyen los datos nos permite evaluar riesgos y beneficios de manera más efectiva. Esto se aplica no solo a compras, sino también en decisiones de salud, educación y finanzas.
2 Comprensión del comportamiento humano
La campana de Gauss también nos ayuda a entender el comportamiento humano. Las características como la inteligencia, la altura y otras habilidades suelen distribuirse normalmente en la población. Esto significa que, al observar un grupo, podemos esperar que la mayoría se encuentre en el medio, con menos individuos en los extremos.
Este conocimiento puede influir en cómo percibimos y evaluamos a los demás, así como en la forma en que diseñamos políticas y programas sociales. Al reconocer que las variaciones son normales, podemos ser más comprensivos y empáticos hacia las diferencias individuales.
¿Qué significa que una distribución sea normal?
Una distribución normal es aquella en la que los datos se distribuyen de manera simétrica alrededor de la media, formando una forma de campana. Esto implica que la mayoría de los datos se agrupan en torno a la media, y hay menos datos en los extremos. La importancia de esta distribución radica en que muchas variables naturales siguen este patrón, lo que permite hacer inferencias y predicciones basadas en ella.
¿Cómo se utiliza la campana de Gauss en la investigación científica?
En la investigación científica, la campana de Gauss se utiliza para analizar datos y hacer inferencias sobre poblaciones a partir de muestras. Los investigadores aplican técnicas como la inferencia estadística y las pruebas de hipótesis, que dependen de la suposición de que los datos siguen una distribución normal. Esto les permite evaluar la significancia de sus hallazgos y formular conclusiones basadas en evidencia.
¿Cuáles son algunas aplicaciones prácticas de la campana de Gauss?
Las aplicaciones de la campana de Gauss son diversas. Se utiliza en el control de calidad en la industria, en estudios psicológicos para analizar pruebas de inteligencia y en encuestas sociales para comprender actitudes y comportamientos. Además, su comprensión es crucial en la toma de decisiones cotidianas, desde compras hasta evaluaciones de riesgo en salud y finanzas.
¿Qué hacer si mis datos no siguen una distribución normal?
Si tus datos no siguen una distribución normal, puedes considerar el uso de transformaciones para normalizarlos o aplicar métodos estadísticos que no dependan de esta suposición. También es recomendable utilizar medidas robustas, como la mediana y el rango intercuartílico, que son menos sensibles a valores atípicos y proporcionan una representación más precisa de los datos.
¿Por qué es importante entender la campana de Gauss en la vida cotidiana?
Entender la campana de Gauss es importante porque nos ayuda a tomar decisiones informadas basadas en datos. Nos permite evaluar riesgos, comprender comportamientos y reconocer patrones en diversas situaciones. Además, al ser conscientes de cómo se distribuyen las características en la población, podemos ser más empáticos y comprensivos hacia las diferencias individuales.
¿Qué es la regla empírica y cómo se relaciona con la campana de Gauss?
La regla empírica, también conocida como la regla del 68-95-99.7, describe cómo se distribuyen los datos en una distribución normal. Indica que aproximadamente el 68% de los datos se encuentran dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones y el 99.7% dentro de tres. Esta regla es fundamental para entender la variabilidad y la dispersión de los datos en contextos estadísticos.
¿Existen distribuciones similares a la campana de Gauss?
Sí, existen varias distribuciones que son similares a la campana de Gauss, pero que tienen características diferentes. Por ejemplo, la distribución t de Student es similar pero se utiliza cuando se trabaja con muestras pequeñas. Otras distribuciones, como la distribución chi-cuadrado y la distribución binomial, tienen formas y propiedades distintas, pero también son útiles en el análisis estadístico.