La distribución normal, también conocida como distribución gaussiana, es uno de los conceptos más fundamentales en la estadística y la probabilidad. Su importancia radica en su capacidad para modelar una amplia variedad de fenómenos en la naturaleza, la ciencia y las ciencias sociales. Desde la altura de las personas hasta los errores de medición, muchas variables tienden a distribuirse de manera normal. En este artículo, exploraremos diversos ejemplos de distribución normal con gráficas que te ayudarán a comprender su aplicación y visualización en distintos contextos. A medida que avancemos, aprenderás a interpretar estas gráficas y a reconocer la relevancia de la distribución normal en situaciones cotidianas y profesionales.
¿Qué es la Distribución Normal?
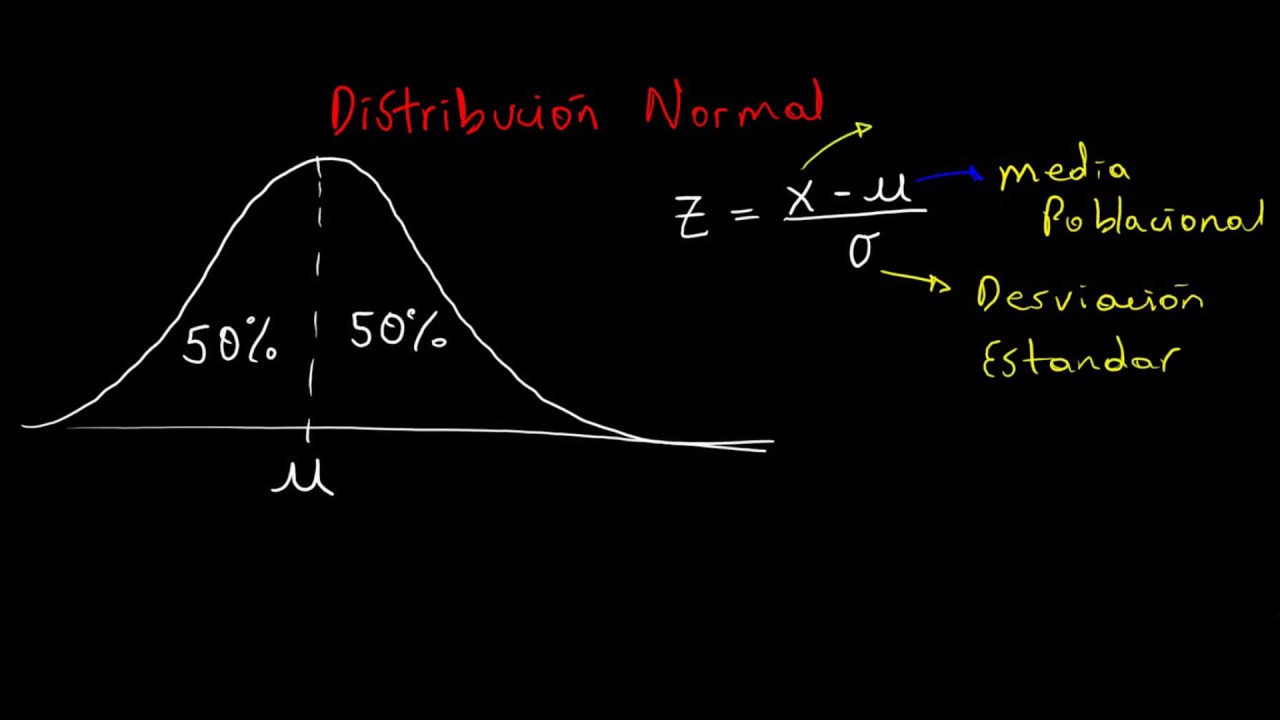
La distribución normal es una función de probabilidad que describe cómo se distribuyen los valores de una variable aleatoria continua. Se caracteriza por su forma de campana, donde la mayoría de los valores se agrupan alrededor de la media, y se extienden hacia los extremos, creando una simetría perfecta. Esta distribución está definida por dos parámetros: la media (μ) y la desviación estándar (σ).
Características Clave de la Distribución Normal
- Simetría: La curva es simétrica respecto a la media, lo que significa que la probabilidad de obtener valores a la izquierda de la media es igual a la probabilidad de obtener valores a la derecha.
- Media, Mediana y Moda: En una distribución normal, la media, la mediana y la moda coinciden en el mismo punto central.
- Regla Empírica: Aproximadamente el 68% de los datos se encuentran dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones y el 99.7% dentro de tres desviaciones.
Visualización de la Distribución Normal
Una gráfica de distribución normal muestra la densidad de probabilidad de los valores en función de su distancia de la media. En una gráfica típica, la x representa los valores de la variable, mientras que la y representa la densidad de probabilidad. A medida que te alejas de la media, la densidad disminuye, reflejando que los valores extremos son menos probables. Esta visualización es fundamental para comprender cómo se comportan los datos en contextos reales.
Ejemplos de Distribución Normal en la Vida Cotidiana
La distribución normal se encuentra en múltiples aspectos de la vida cotidiana. Aquí exploraremos algunos ejemplos que ilustran cómo esta distribución se manifiesta en diferentes contextos.
Altura de la Población
Uno de los ejemplos más comunes de distribución normal es la altura de las personas. Si tomamos una muestra grande de individuos, la altura tiende a distribuirse normalmente alrededor de una media. Por ejemplo, en una población adulta, podemos encontrar que la media de altura es de 1.70 metros, con una desviación estándar de 10 cm. Esto significa que la mayoría de las personas medirán entre 1.60 y 1.80 metros, y los extremos serán menos frecuentes.
Resultados de Exámenes
Los resultados de exámenes estandarizados, como el SAT o el GRE, también tienden a seguir una distribución normal. Supongamos que un examen tiene una media de 500 puntos y una desviación estándar de 100 puntos. En este caso, la mayoría de los estudiantes obtendrán puntajes cercanos a la media, mientras que muy pocos alcanzarán puntajes extremadamente bajos o altos. Esto permite a las instituciones educativas establecer umbrales de admisión basados en la posición relativa de un estudiante en la distribución.
Errores de Medición
En experimentos científicos, los errores de medición a menudo se distribuyen normalmente. Imagina que estás midiendo la longitud de un objeto con una regla. Si repites la medición múltiples veces, es probable que los resultados se agrupen alrededor de la longitud verdadera del objeto, con errores menores distribuidos normalmente alrededor de esa media. Esto es crucial para evaluar la precisión y la confiabilidad de los experimentos.
Aplicaciones de la Distribución Normal en el Mundo Profesional
La distribución normal no solo es útil en la vida cotidiana, sino que también tiene aplicaciones significativas en el ámbito profesional. Vamos a explorar algunas de estas aplicaciones.
Finanzas y Economía
En el ámbito financiero, la distribución normal se utiliza para modelar el comportamiento de los precios de las acciones y otros activos. Los analistas utilizan esta distribución para evaluar el riesgo y la volatilidad de los activos. Por ejemplo, si un analista determina que los retornos de una acción siguen una distribución normal con una media del 5% y una desviación estándar del 2%, puede predecir que hay un 68% de probabilidad de que el retorno esté entre 3% y 7% en un año determinado.
Control de Calidad
Las empresas utilizan la distribución normal en el control de calidad para garantizar que los productos cumplan con estándares específicos. Al medir características como el peso o las dimensiones de un producto, las empresas pueden aplicar la regla empírica para determinar cuántos productos están dentro de las especificaciones. Si la media del peso de un lote de productos es de 500 gramos con una desviación estándar de 5 gramos, la empresa puede estar segura de que la mayoría de los productos cumplen con los requisitos establecidos.
Investigación de Mercados
La distribución normal también se utiliza en la investigación de mercados para analizar las preferencias de los consumidores. Las encuestas a menudo generan resultados que se distribuyen normalmente. Por ejemplo, si se pregunta a los consumidores sobre su satisfacción con un producto en una escala del 1 al 10, los resultados tienden a agruparse alrededor de un puntaje medio, lo que permite a las empresas identificar áreas de mejora y oportunidades de crecimiento.
Interpretación de Gráficas de Distribución Normal
Entender cómo interpretar gráficas de distribución normal es esencial para aplicar este concepto en diversas disciplinas. Las gráficas muestran la densidad de probabilidad y cómo se distribuyen los datos en relación con la media.
Ejes de la Gráfica
En una gráfica de distribución normal, el eje horizontal (x) representa los valores de la variable que estamos estudiando, mientras que el eje vertical (y) representa la densidad de probabilidad. Es importante observar cómo se distribuyen los datos a lo largo de la curva. Las áreas bajo la curva representan la probabilidad de que un valor caiga dentro de un rango específico. Por ejemplo, el área bajo la curva entre una desviación estándar a cada lado de la media representa aproximadamente el 68% de los datos.
Identificación de la Media y la Desviación Estándar
Al observar una gráfica, puedes identificar fácilmente la media, que es el punto más alto de la curva. La desviación estándar se puede visualizar a través del ancho de la curva: una desviación estándar más pequeña resultará en una curva más estrecha, mientras que una mayor producirá una curva más ancha. Esta visualización te permite entender la variabilidad de los datos y cómo se distribuyen alrededor de la media.
Uso de Z-Scores
Los Z-scores son una herramienta útil para interpretar la posición de un valor específico en relación con la media. Un Z-score indica cuántas desviaciones estándar se encuentra un valor de la media. Por ejemplo, un Z-score de +2 significa que el valor está dos desviaciones estándar por encima de la media, lo que representa un valor relativamente raro en una distribución normal. Esta información es valiosa en diversas aplicaciones, desde la evaluación de desempeño hasta la identificación de outliers en un conjunto de datos.
¿Qué es una distribución normal?
La distribución normal es una función de probabilidad que describe cómo se distribuyen los valores de una variable aleatoria continua. Se caracteriza por su forma de campana, donde la mayoría de los valores se agrupan alrededor de la media, y su simetría respecto a esta. Es fundamental en estadística debido a su capacidad para modelar muchos fenómenos naturales y sociales.
¿Cómo se representa gráficamente una distribución normal?
Una distribución normal se representa gráficamente mediante una curva en forma de campana. En esta gráfica, el eje horizontal muestra los valores de la variable, mientras que el eje vertical representa la densidad de probabilidad. La media se encuentra en el punto más alto de la curva, y la forma de la gráfica está determinada por la media y la desviación estándar.
¿Cuáles son algunos ejemplos de fenómenos que siguen una distribución normal?
Algunos ejemplos comunes incluyen la altura de las personas, los resultados de exámenes estandarizados, los errores de medición en experimentos y el rendimiento de inversiones financieras. En cada uno de estos casos, al observar una gran cantidad de datos, se puede notar que tienden a agruparse alrededor de una media específica, formando una distribución normal.
¿Qué es la regla empírica en la distribución normal?
La regla empírica, también conocida como la regla de 68-95-99.7, establece que en una distribución normal, aproximadamente el 68% de los datos se encuentran dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones estándar y el 99.7% dentro de tres desviaciones estándar. Esta regla es útil para entender la dispersión de los datos en relación con la media.
¿Cómo se utiliza la distribución normal en el ámbito profesional?
En el ámbito profesional, la distribución normal se utiliza en finanzas para modelar el comportamiento de los precios de activos, en control de calidad para evaluar la conformidad de productos y en investigación de mercados para analizar las preferencias de los consumidores. Su capacidad para describir fenómenos de manera precisa la convierte en una herramienta valiosa en diversas disciplinas.
¿Qué son los Z-scores y cómo se utilizan?
Los Z-scores son una medida que indica cuántas desviaciones estándar se encuentra un valor de la media en una distribución normal. Se utilizan para evaluar la posición de un valor específico en relación con el resto de los datos. Un Z-score positivo indica que el valor está por encima de la media, mientras que uno negativo indica que está por debajo. Esta medida es útil para identificar outliers y evaluar el rendimiento en diferentes contextos.
¿Qué pasa si los datos no siguen una distribución normal?
Si los datos no siguen una distribución normal, se pueden utilizar otros modelos de distribución, como la distribución binomial, Poisson o exponencial, dependiendo de la naturaleza de los datos. También se pueden aplicar transformaciones a los datos para intentar normalizarlos o utilizar técnicas estadísticas no paramétricas que no asumen normalidad. Es importante elegir el enfoque adecuado según el contexto y los objetivos del análisis.