En el mundo de la estadística, el coeficiente de correlación se erige como una herramienta fundamental para entender las relaciones entre variables. Ya sea en investigaciones científicas, análisis de mercado o estudios sociales, medir la fuerza y dirección de una relación puede proporcionar información valiosa. Pero, ¿cómo podemos validar estas correlaciones? Aquí es donde entran en juego las pruebas para el coeficiente de correlación. En este artículo, exploraremos los métodos más utilizados para evaluar la significancia de las correlaciones, así como sus aplicaciones prácticas en diferentes campos. Desde el cálculo del coeficiente de Pearson hasta pruebas no paramétricas, descubrirás cómo y cuándo utilizar cada método, así como ejemplos que ilustran su relevancia en la vida cotidiana. Prepárate para adentrarte en el fascinante mundo de las correlaciones y su análisis.
¿Qué es el Coeficiente de Correlación?
El coeficiente de correlación es un valor que mide la relación entre dos variables. Este valor puede oscilar entre -1 y 1, donde:
- 1 indica una correlación positiva perfecta: a medida que una variable aumenta, la otra también lo hace.
- -1 indica una correlación negativa perfecta: a medida que una variable aumenta, la otra disminuye.
- 0 sugiere que no hay correlación entre las variables.
Existen varios tipos de coeficientes de correlación, pero los más comunes son el coeficiente de Pearson y el coeficiente de Spearman. Cada uno tiene sus propias características y se utiliza en diferentes situaciones. Entender la naturaleza de los datos y el contexto del análisis es crucial para elegir el método adecuado.
Coeficiente de Pearson
El coeficiente de Pearson, representado como «r», es una medida que evalúa la relación lineal entre dos variables continuas. Se calcula utilizando la fórmula:
r = Σ((X - X̄)(Y - Ȳ)) / √(Σ(X - X̄)² * Σ(Y - Ȳ)²)Donde X y Y son las variables en cuestión, y X̄ y Ȳ son las medias de cada variable. Este coeficiente es especialmente útil cuando se asume que las variables tienen una distribución normal. Sin embargo, es importante destacar que Pearson solo mide relaciones lineales; si la relación es no lineal, este coeficiente puede no ser representativo.
Coeficiente de Spearman
El coeficiente de Spearman es una alternativa no paramétrica al coeficiente de Pearson. Se utiliza cuando los datos no cumplen con los supuestos de normalidad o cuando las variables son ordinales. Spearman evalúa la relación entre las posiciones (rango) de los datos en lugar de sus valores absolutos. Se calcula mediante la fórmula:
ρ = 1 - (6Σd²) / (n(n² - 1))Donde d es la diferencia entre los rangos de las variables y n es el número de observaciones. Este método es especialmente útil en ciencias sociales y en situaciones donde se trabaja con escalas de clasificación.
Pruebas de Significancia para el Coeficiente de Correlación
Una vez que se ha calculado el coeficiente de correlación, el siguiente paso es determinar si esta correlación es estadísticamente significativa. Esto se hace comúnmente a través de pruebas de hipótesis. Generalmente, se establece la hipótesis nula (H0) que afirma que no existe correlación (r = 0) y la hipótesis alternativa (H1) que sugiere que sí hay una correlación (r ≠ 0).
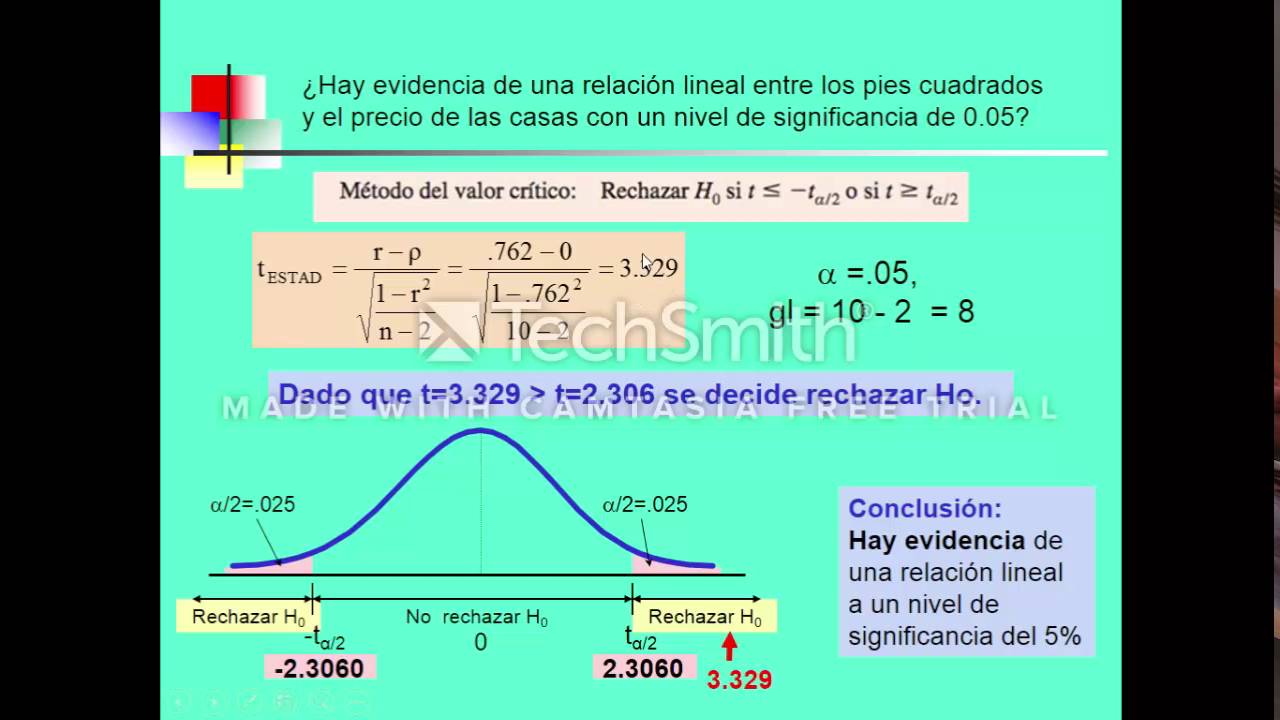
Para llevar a cabo esta prueba, se puede utilizar el valor t, que se calcula de la siguiente manera:
t = r√(n - 2) / √(1 - r²)Donde n es el número de observaciones. Este valor t se compara con un valor crítico de una tabla t para determinar la significancia. Si el valor t es mayor que el valor crítico, se rechaza la hipótesis nula.
Prueba de Pearson
La prueba de Pearson se aplica cuando se ha utilizado el coeficiente de correlación de Pearson. Es fundamental asegurarse de que los datos sean independientes y que se distribuyan normalmente. Una vez que se ha calculado el valor t, se puede determinar la significancia mediante un nivel de confianza, comúnmente establecido en 0.05. Esto significa que hay un 5% de probabilidad de cometer un error tipo I al rechazar la hipótesis nula.
Prueba de Spearman
Similar a la prueba de Pearson, la prueba de Spearman también requiere que se calcule un valor t, pero se basa en los rangos en lugar de los valores absolutos. La interpretación de los resultados es análoga: si el valor t supera el umbral crítico, se puede concluir que existe una correlación significativa entre las variables analizadas.
Aplicaciones Prácticas del Coeficiente de Correlación
Las pruebas para el coeficiente de correlación tienen numerosas aplicaciones en diversas disciplinas. A continuación, exploramos algunas de las más relevantes:
En el ámbito científico
En investigaciones científicas, el coeficiente de correlación se utiliza para validar hipótesis sobre la relación entre variables. Por ejemplo, en estudios médicos, se puede analizar la correlación entre el consumo de ciertos alimentos y el riesgo de enfermedades. Un coeficiente alto podría indicar que hay una relación que merece ser investigada más a fondo.
En el análisis de mercado
Las empresas utilizan el coeficiente de correlación para evaluar cómo diferentes factores, como el precio y la demanda, están relacionados. Esto les ayuda a tomar decisiones informadas sobre precios y estrategias de marketing. Por ejemplo, un análisis podría revelar que a medida que disminuye el precio de un producto, la demanda aumenta, lo que podría llevar a ajustes en la estrategia de ventas.
En educación
Los educadores pueden utilizar el coeficiente de correlación para analizar el rendimiento académico de los estudiantes en relación con diversas variables, como el tiempo de estudio o la asistencia a clases. Esto puede proporcionar información valiosa sobre qué factores contribuyen al éxito académico y permitir la implementación de estrategias más efectivas.
Limitaciones del Coeficiente de Correlación
A pesar de su utilidad, el coeficiente de correlación tiene sus limitaciones. Una de las principales es que no implica causalidad. Una correlación significativa no significa que una variable cause cambios en otra. Por ejemplo, si se encuentra una correlación entre el aumento de las temperaturas y el consumo de helados, no se puede concluir que uno cause el otro, ya que ambos pueden estar influenciados por un tercer factor, como la temporada de verano.
Además, la correlación es sensible a valores atípicos. Un único dato extremo puede distorsionar significativamente el coeficiente, llevando a interpretaciones erróneas. Por lo tanto, es esencial realizar un análisis de datos previos y considerar la eliminación de outliers antes de calcular el coeficiente de correlación.
Correlaciones espurias
Las correlaciones espurias son otro problema común. Estas ocurren cuando dos variables están correlacionadas, pero no hay una relación causal entre ellas. Por ejemplo, un estudio puede encontrar que hay una correlación entre el número de piratas y la temperatura global. Aunque ambas variables pueden mostrar una tendencia similar, esto no implica que una cause la otra. Identificar y controlar estas situaciones es crucial para obtener resultados válidos y significativos.
Cómo Interpretar el Coeficiente de Correlación
La interpretación del coeficiente de correlación debe hacerse con cuidado. Un valor cercano a 1 o -1 indica una relación fuerte, mientras que valores cercanos a 0 sugieren una relación débil. Sin embargo, la magnitud de la correlación no siempre refleja la importancia práctica de la relación. Es esencial considerar el contexto y la relevancia de la correlación en el campo específico de estudio.
Además, es recomendable complementar el análisis del coeficiente de correlación con visualizaciones, como diagramas de dispersión, que permiten observar la relación entre las variables de manera más clara. Esto puede ayudar a identificar patrones, tendencias y posibles outliers que podrían afectar los resultados del análisis.
¿Qué es el coeficiente de correlación y por qué es importante?
El coeficiente de correlación mide la relación entre dos variables, indicando si aumentos en una variable están relacionados con aumentos o disminuciones en otra. Es importante porque permite a investigadores y analistas entender y cuantificar relaciones, lo que puede influir en decisiones y estrategias en diversas áreas, desde la ciencia hasta los negocios.
¿Cuáles son las diferencias entre el coeficiente de Pearson y el coeficiente de Spearman?
El coeficiente de Pearson mide la relación lineal entre dos variables continuas, mientras que el coeficiente de Spearman evalúa la relación entre rangos, siendo más adecuado para datos no paramétricos o cuando las variables son ordinales. En resumen, Pearson es más restrictivo en sus supuestos, mientras que Spearman es más flexible.
¿Cómo se determina si una correlación es significativa?
Para determinar la significancia de una correlación, se realiza una prueba de hipótesis donde se establece una hipótesis nula que asume que no hay correlación. Se calcula un valor t y se compara con un valor crítico en una tabla t. Si el valor t es mayor que el crítico, se rechaza la hipótesis nula, indicando que la correlación es significativa.
¿Qué limitaciones tiene el coeficiente de correlación?
Las principales limitaciones incluyen que no implica causalidad, es sensible a valores atípicos y puede dar lugar a correlaciones espurias. Esto significa que es fundamental interpretar los resultados en el contexto adecuado y complementarlos con análisis adicionales y visualizaciones.
¿Puedo usar el coeficiente de correlación para datos categóricos?
No es recomendable utilizar el coeficiente de correlación para datos categóricos, ya que este método está diseñado para variables continuas. Sin embargo, existen otras técnicas, como el análisis de chi-cuadrado, que son más apropiadas para evaluar relaciones entre variables categóricas.
¿Qué es una correlación espuria?
Una correlación espuria ocurre cuando dos variables están correlacionadas, pero no existe una relación causal entre ellas. Esto puede suceder debido a la influencia de un tercer factor. Es importante identificar y considerar estas situaciones al analizar datos para evitar conclusiones erróneas.
¿Cómo puedo visualizar la relación entre dos variables?
Una de las mejores formas de visualizar la relación entre dos variables es mediante un diagrama de dispersión. Este gráfico muestra puntos que representan pares de valores de las dos variables, lo que permite observar patrones, tendencias y posibles outliers que podrían afectar el análisis de correlación.